Beta (β)
Seguimos con otro coeficiente muy utilizado y que forma parte del modelo CAMP, que bien se denomina la Beta del activo o proyecto o coeficiente de volatilidad del activo o proyecto. En adquisición de empresas reflejará el rendimiento esperado de la empresa.
Hoy quiero hablarte del concepto y definición de la Beta en finanzas. Un elemento indispensable para calcular el Coste del Capital o reflejar el rendimiento de un activo y el comportamiento que dispondrá en un mercado de referencia. Así que, despeja tu mente y sigue este artículo, intentaré darte la mejor explicación posible para entenderlo. Sin más, comencemos.
¿Qué es la Beta en finanzas?
Cuando hablamos de la beta (β) de un activo o proyecto, estamos hablando del rendimiento de dicho activo con respecto a un índice de referencia. Por tanto, la beta (β), reflejará el grado de volatilidad del activo, por decirlo de otra manera, es el grado de riesgo por cada fluctuación que tenga el rendimiento del mercado. Si lo queremos decir de manera más coloquial, a mayor beta, mayor será el riesgo que deberá asumir el inversor, por lo que deberá exigir mayor rendimiento.
Pero la (β) no deja de ser una estimación, dado que dicho rendimiento se calcula de datos obtenidos anteriormente, ya sean rendimientos diarios, mensuales o anuales que haya tenido el activo. El resultado obtenido será, pues, una estimación de su rendimiento.
Fórmula Beta de un activo o proyecto
La fórmula para obtener la Beta de un activo o empresa, se ha de calcular siguiendo la siguiente fórmula.
β = σi / σ²m
- σi: Covarianza de un activo y la del mercado
- σ²m: varianza del mercado
En esta fórmula, podemos obtener tres situaciones:
- β > 1: Títulos o activos con mayor volatilidad, es decir, si sube el valor del índice, tendrá una mayor proporción de subida y si el valor del índice disminuye, la baja será mayor proporcionalmente.
- β = 1: Activos sin riesgo, sería igual al Rf, se percibirá la misma rentabilidad en proporción al valor del índice
- β < 1: Activos defensivos, dispone de menos variaciones cuando varía el valor del índice.
¿Cómo calcular la beta de un activo o proyecto?
Para ello necesitaremos el Excel y crear una gráfica de dispersión y también necesitaremos el rendimiento del activo objetivo y el índice de referencia por la que vamos a estimar.
Si lo que quieres es ir más rápido, las betas puedes obtenerlos en el Informe mensual Sociedad de Bolsas en el caso de la Bolsa de Madrid. Aquí tienes un PDF de los datos mensuales de agosto de 2018 en el que podrás ver las betas a partir de la página 22. Pero de nada vale saber donde encontrar las betas de las empresas sin saber su procedencia.
Para no irme muy lejos, voy a hacer un ejercicio de una empresa que cotiza en el IBEX 35 y que calcularé los rendimientos obtenidos con respecto a este mismo de los últimos 20 días. Es un periodo muy pequeño pero suficiente para aplicar la teoría.
En el excel debemos agrupas los diferentes rendimientos, en el eje x, tendremos que indicar los rendimientos obtenidos de las acciones por las últimas 20 sesiones y en el eje y, el rendimiento obtenido de las últimas 20 sesiones del índice IBEX 35.
Pero lo que nos va a interesar no va a ser el precio de cierre, más bien el retorno de un día para otro.
| Fecha | Eje Y BBVA | Retorno (Dn/Dn-1) | Eje X Ibex35 | Retorno (Dn/Dn-1) |
| 21/09/2018 | 5,636 | 9.590,40 | ||
| 20/09/2018 | 5,678 | -0,74% | 9.583,70 | 0,07% |
| 19/09/2018 | 5,596 | 1,47% | 9.486,30 | 1,03% |
| 18/09/2018 | 5,486 | 2,01% | 9.447,50 | 0,41% |
| 17/09/2018 | 5,503 | -0,31% | 9.404,60 | 0,46% |
| 14/09/2018 | 5,449 | 0,99% | 9.365,30 | 0,42% |
| 13/09/2018 | 5,438 | 0,20% | 9.329,20 | 0,39% |
| 12/09/2018 | 5,215 | 4,28% | 9.306,80 | 0,24% |
| 11/09/2018 | 5,209 | 0,12% | 9.284,10 | 0,24% |
| 10/09/2018 | 5,199 | 0,19% | 9.270,80 | 0,14% |
| 07/09/2018 | 5,180 | 0,37% | 9.171,20 | 1,09% |
| 06/09/2018 | 5,228 | -0,92% | 9.208,70 | -0,41% |
| 05/09/2018 | 5,363 | -2,52% | 9.301,30 | -1,00% |
| 04/09/2018 | 5,368 | -0,09% | 9.376,30 | -0,80% |
| 03/09/2018 | 5,354 | 0,26% | 9.376,10 | 0,00% |
| 31/08/2018 | 5,370 | -0,30% | 9.399,10 | -0,24% |
| 30/08/2018 | 5,381 | -0,20% | 9.467,60 | -0,72% |
| 29/08/2018 | 5,530 | -2,69% | 9.569,50 | -1,06% |
| 28/08/2018 | 5,490 | 0,73% | 9.606,50 | -0,39% |
| 27/08/2018 | 5,571 | -1,45% | 9.659,80 | -0,55% |
Covarianza Rendimiento del activo y Rendimiento del índice
El siguiente paso será calcular en la covarianza de los intervalos del retorno del BBVA y del IBEX35, siendo.

Suponiendo que la columna del retorno BBVA sea C y empiece desde C3 y la columna del retorno del IBEX 35 sea E y empiece por E3, en excel, la fórmula a aplicar sería la siguiente:
=COVAR(C3:C21;E3:E21) = 0,0000564686427
Varianza del rendimiento del índice
Tras calcular la covarianza, solo nos quedará calcular la varianza del índice IBEX 35 del mismo periodo, siendo.

En Excel y bajo los mismos supuestos anteriores, sería:
=VAR(E3:E21) = 0,00003900813682
Obtención de la Beta financiera
Una vez tengamos la covarianza de los rendimientos obtenidos del activo, del mercado de referencia y además la varianza del mercado de referencia, el siguiente paso es realizar la división entre una sobre otra para obtener así la beta, siendo.
Beta= Covarianza (Activo y Mercado)/ Varianza Mercado
¿Cómo afecta la beta y la prima de riesgo en los activos o proyectos?
Para una explicación más gráfica, te voy a hablar de caballos y de representación gráfica para los que no le gusten mucho los caballos cuando la beta actúa como multiplicador de la prima de riesgo y de esta manera tener un mayor concepto.
Para entender mejor, de la fórmula del CAMP, voy a calcular lo señalado en rojo, es decir, el cálculo de la prima de riesgo del propio activo.
CAMP = Rf + βc*(Em-Rf)
En donde...
- Rf: Rendimiento del activo sin riesgo, es decir, la tasa libre de riesgo
- Em: Rendimiento esperado del mercado
- (Em-Rf): Prima de riesgo del mercado
- βc: Rendimiento del mercado del activo o proyecto
¿Cómo calcular la beta de empresa que no cotiza en bolsa?
Si has seguido y llegado hasta aquí, te habrás dado cuenta de que la beta es fácil de calcular porque ya dispones de los datos, solo es necesario aplicar la fórmula y es aquí cuando puede que te preguntes cómo se calcula la beta si la empresa no cotiza en bolsa.
El grueso de las empresas no cotizan en la bolsa, por lo que el cálculo de la beta de empresas no cotizadas resulta un tanto importante para los que deseen valorar empresas de estas características por diversas circunstancias. Esto será posible gracias a la utilización del método Hamada
Para calcular el valor de una beta de una empresa que no cotiza se ha de seguir los siguientes paso:
- Tomar referencia de varias empresas con características iguales que coticen en la bolsa
- Calcular las betas de las compañías que cotizan en bolsa
- Desapalancar las betas: Porque la beta obtenida de mencionadas compañías tienen como referencia las deudas y para esto es necesario estimar la beta cuando la deuda es 0.
- Calcular una beta media ponderada entre los diferentes empresas cotizantes
- Apalancar la beta media con la estructura financiera de la compañía que no cotiza
- Realizar una media ponderada de las betas obtenidas, se tendrá tantas betas como tantas empresas cotizantes se hayan usado de referencia. Al hacer la media dispondremos de una beta media ponderada.
- Aplicar el Modelo CAMP más la suma de una prima por tamaño y liquidez
Es decir, lo que intenta el método Hamada es calcular la beta sin deudas de las empresas cotizantes, obtener una media ponderada de cada una y luego calcular la beta apalancada, pero con base en la deuda de la empresa que no cotiza.
Si te has mareado por los pasos anteriores, no te preocupes, voy a ponerte un ejemplo y aplicar una fórmula que no te he indicado anteriormente y es
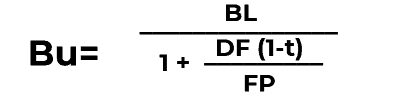
En donde...
- Bu = Beta desapalancada
- BL = Beta apalancada
- DF = Deuda Financiera
- t = tipo impositivo
- FP = Fondos Propios
Aplicación del método Hamada
Si te has fijado antes, lo que te pide la fórmula sería la beta apalancada de cada una de las empresas, así como su deuda financiera y los fondos propios y claro está, el tipo impositivo a la que recae la deuda financiera. Ahora vamos a imaginar que tenemos una empresa que cotiza en bolsa y que tiene una cierta similitud con la empresa que no cotiza.
Tomar referencia de varias empresas con características iguales que coticen en la bolsa
Dicha empresa dispone de los siguientes datos.
| Fondos propios | Deuda Financiera | Beta | Tipo interés | Beneficios |
| 15.000.000 | 7.000.000 | 1,1 | 0.20 | 4.0000.0000 |
Calcular las betas de las compañías que cotizan en bolsa
Este punto no sería necesario porque ya se ha obtenido previamente y figura en la tabla
| Fondos propios | Deuda Financiera | Beta | Tipo interés |
| 15.000.000 | 7.000.000 | 1,1 | 0.20 |
Desapalancar las betas
Aplicaremos la fórmula para desapalancar la beta de la empresa
Bu = 1,1 / 1+ ((7.000.000(1-0,20))/15.000.000)
Beta desapalancada = 0.8
Calcular una beta media ponderada entre los diferentes empresas cotizantes
Este punto también podemos saltarnos, en nuestro simple ejemplo dado que solo hemos cogido una empresa, por lo que la media ponderada será el resultado obtenido.
Apalancar la beta media con la estructura financiera de la compañía que no cotiza
Para este punto, tendremos que saber la estructura financiera de la empresa que no cotiza, siendo los siguientes
| Fondos propios | Deuda Financiera | Tipo impositivo |
| 13.000.000 | 8.000.000 | 0.25 |
Seguiremos la siguiente fórmula:
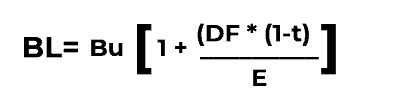
En donde...
- BL = Beta apalancada
- Bu = Beta desapalancada
- DF = Deuda Financiera
- t = Tipo impositivo
- E = Estructura de los fondos propios o Fondos Propios
Sustituyendo, tendremos lo siguiente
Bl = 0.8 * (1+(8.0000.000*(1-0,25))/13.000.000)
Bl= 0,8 * 1.46 = 1,17
Con esto ya obtendríamos al beta de una empresa que no cotiza en bolsa
-
Muy Didáctico y simple de Entender
Fui profesor de Finanzas y yo Enseñaba estas cosas hace varios Años
Voy a recomendar la compra de Acciones a un
Amigo y el portal financiero que utilizó muestra las betas de las Acciones y recordé perfectamente el Cálculo y lo que significa
1 Te puede interesar
Deja una respuesta

Entradas relacionadas